Good! Why Is The Triangle Inequality Theorem Important
A c b. According to this theorem for any triangle the sum of lengths of two sides is always greater than the third side.
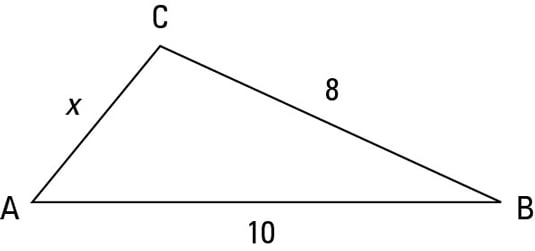
Using The Triangle Inequality Principle Dummies
This is because going from A to C by way of B is longer than going.

Why is the triangle inequality theorem important. The Triangle Inequality Theorem is just a more formal way to describe what we just discovered. The task also reinforces the concepts of equivalence and inequivalence. 58 U V 62 Use sum to find m T.
4 8 10 4 8 10 4 10 8 8 10 4. In a Euclidean space the sum of measures of these three angles of any triangle is invariably equal. The triangle inequality theorem describes the relationship between the three sides of a triangle.
Triangular inequality Theorem is important to know if the triangle with the three measurements provided or not. B c a. In a triangle the side opposite to the largest side is greatest in measure.
The converse of the above theorem is also true according to which in a triangle the side opposite to a greater angle is the longest side of the. It follows from the fact that a straight line is the shortest path between two points. The triangle inequality theorem is one of the important mathematical principles that is used across various branches of mathematics.
For example the triangle with sides 3 units 4 units and 9 units does not exist as it does not meet the triangular inequality theorem. The inequality is strict if the triangle is non- degenerate meaning it has a non-zero area. Check whether it is possible to have a triangle with the given side lengths.
Also AB AC CB. This is because those line segments satisfy the triangle inequality theorem. In real life civil engineers use the triangle inequality theorem since their area of work deals with surveying transportation and urban planning.
A 3ft 7ft 8ft. So in a triangle ABC AC AB BC. Any side of a triangle must be shorter than the other two sides added together.
The inequality properties of a triangle are. Triangle inequality theorem statementTriangle inequality in finding lengths of the sidesTriangle inequality helps in finding whether the given measurements m. Sum of any any pair of sides must be greater than the third side.
Well imagine one side is not shorter. 1 d x x 0. Therefore a triangle inequality theorem is a useful tool for checking whether a given set of three dimensions will form a triangle or not.
The sum of each pair of side lengths is greater than the third length. It is not an inevitable rule of metric space so much so that it forms the basis for our definition of metric and hence naturally forms the underpinning of metric spaces. The triangle inequality theorem states that the length of any of the sides of a triangle must be shorter than the lengths of the other two sides added together.
12 10 1418 8 4 Conclusion. When side lengths are equal a degenerate triangle is formed which is an interesting discussion that can be had with students. The absolute value of a sum is less than or equal to the sum of the absolute values for any two real numbers.
The triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side. In a triangle the length of any side is less than the sum of the other two sides. The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Simply put it will not form a triangle if the above 3 triangle inequality conditions are false. Students will be able to decide if three lengths can make a triangle. Students will be able to find the range of possible lengths of the third side when given two sides.
When the sum of a pair of sides is equal to th. Why triangular inequality Important theorem. A b c.
As the theorem states that sum of any two sides should be greater than the measurement of the third side. The triangle inequality theorem helps them to calculate the unknown lengths and. The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side.
Understand the triangle inequality theorem by discovering the relationship between angles and their opposite segments in a triangle About this lesson. The triangle inequality theorem is important to find out whether the triangle with the given three measurements exists or not. We found that when you put the two short sides end to end thats the sum of the two shortest sides they must be longer than the longest side thats why theres a.
If a side is equal to the other two sides it is not a triangle just a straight line back and forth. BC BA AC This is an important theorem for it says in effect that the shortest path between two points is the straight line segment path. Try moving the points below.
B c a. The following are the triangle inequality theorems. Difference of any pair of sides must be greater than the third side.
A c b. The triangle inequality theorem states that the length of any of the sides of a triangle must be shorter than the lengths of the other two sides added together. Can a triangle have sides with the given lengths.
This rule must be satisfied for all 3. It is not an inevitable rule of metric space so much so that it forms the basis for our definition of metric and hence naturally forms the underpinning of metric spaces. As theorema states that sum of any two sides should be higher than the third side measurement.
The definition of a metric. In the figure the following inequalities hold. Triangle inequality states that the sum of the two sides needs to be greater than or equal to the third side.
Triangle Inequality is a characterization for the shortest path. Example 1Use the Triangle Inequality Theorem to tell whether a triangle can have sides with the given lengths. M T 60 so U is smallest Therefore VT is shortest T Theorem 5-12 The Triangle Inequality Theorem The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Ab is less than or equal to ab. Let us consider the triangle. What is the sum of all 3 sides of a triangle.
If a side is longer then the other two sides dont meet. Triangle Inequality is a characterization for the shortest path.
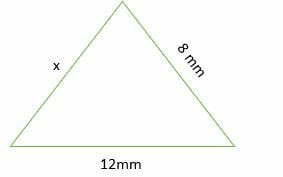
Triangle Inequality Explanation Examples

The Triangle Inequality By The End Of This Lesson You Should Be Able
What S The Triangle Inequality Theorem Gmat Rockstar

Triangle Inequality Brilliant Math Science Wiki

Triangle Inequality Theorem Proof And Examples

Triangle Inequality Brilliant Math Science Wiki

Triangle Inequality Theorem Definition Formula Proof Examples

Triangle Inequality Theorem Kate S Math Lessons

Inequalities In One Triangle Video Lesson Transcript Study Com

Triangle Inequality Theorem Definition Formula Proof Examples

Triangle Inequality Theorem Definition Formula Proof Examples
Can A Triangle Be Formed With Sides Lengths Of 6 Cm 2 Cm And 8 Cm Quora

The Triangle Inequality Theorem Interactive Notebook Page For Geometry Triangle Inequality Math Teaching Math
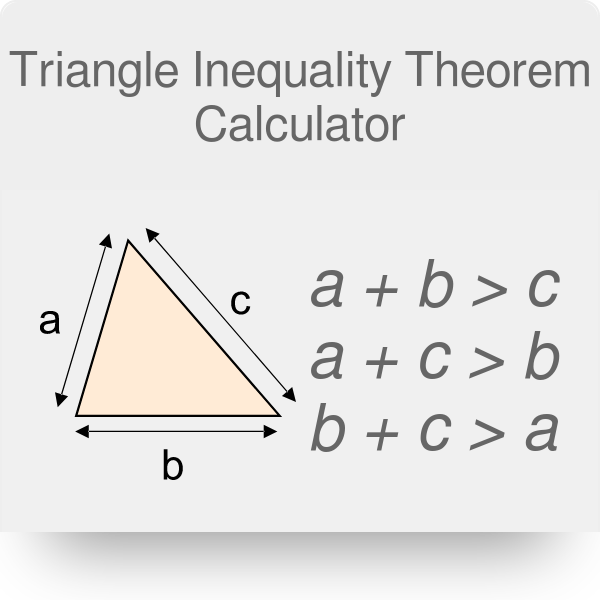
Triangle Inequality Theorem Calculator

Triangle Inequality Theorem Definition Formula Proof Examples

Triangle Inequality Theorem Definition Formula Proof Examples
Triangle Inequality Theorem Geogebra

Triangle Inequality Theorem Proofs Study Com
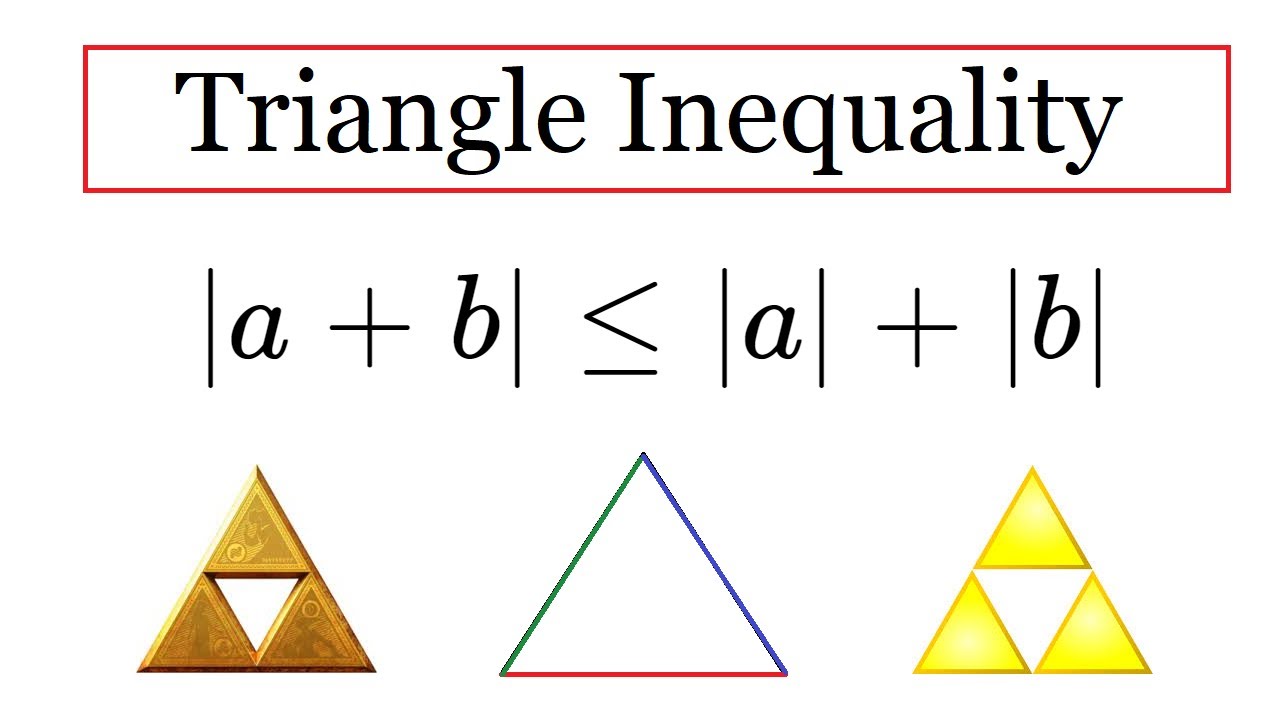
Comments
Post a Comment